Una ecuación es
una igualdad matemática entre
dos expresiones,
denominadas miembros y separadas por el signo igual, en las que aparecen
elementos conocidos o datos desconocidos
o incógnitas, relacionados mediante operaciones matemáticas.
Los valores conocidos
pueden ser números, coeficientes o constantes; también variables o incluso
objetos complejos como funciones o vectores, los elementos desconocidos pueden
ser establecidos mediante otras ecuaciones de un sistema, o algún otro
procedimiento de resolución de ecuaciones.
Las incógnitas, representadas generalmente por letras, constituyen los valores
que se pretende hallar (en ecuaciones complejas en lugar de valores numéricos
podría tratarse de elementos de un cierto conjunto abstracto, como sucede en
las ecuaciones diferenciales). Por
ejemplo, en la ecuación algebraica siguiente:
La variable x representa
la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes
conocidas. La igualdad planteada por una ecuación será cierta o falsa
dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar
entonces que una ecuación es una igualdad condicional, en la que solo ciertos
valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una
ecuación a cualquier valor individual de dichas variables que la satisface.
Para el caso dado, la solución es:
TIPOS
DE ECUACIONES
1.
Ecuaciones polinómicas
1.1 Ecuaciones polinómicas enteras
Las ecuaciones polinómicas son de la forma P(x) =
0, donde P(x) es un polinomio.
1.1.1 Ecuaciones de primer grado o lineales
Son del tipo ax + b
= 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer
términos y simplificar adoptan esa expresión.
(x
+ 1)2 = x2 - 2
x2 +
2x + 1 = x2 - 2
2x
+ 1 = -2
2x
+ 3 = 0
1.1.2 Ecuaciones de segundo grado o
cuadráticas
Son ecuaciones del tipo ax2 + bx + c = 0,
con a ≠ 0.
Ecuaciones de segundo grado incompletas
ax2 =
0
ax2 +
b = 0
ax2 +
bx = 0
1.1.3
Ecuaciones de tercer grado
Son ecuaciones del
tipo ax3 + bx2 + cx + d = 0, con a ≠ 0.
1.1.4
Ecuaciones de cuarto grado
Son ecuaciones del
tipo ax4 + bx3 + cx2 + dx + e = 0, con a ≠ 0.
Ecuaciones bicuadradas
Son ecuaciones de cuarto grado que no tiene términos
de grado impar.
ax4 + bx2 + c = 0, con a ≠ 0.
1.1.5 Ecuaciones de grado n
En general, las ecuaciones de grado n son de la forma:
a1xn + a2xn-1 + a3xn-2 + ...+ a0 =
0
1.2. Ecuaciones polinómicas racionales
Las ecuaciones polinómicas son de la forma:
donde P(x) y Q(x) son polinomios.
1.3.
Ecuaciones polinómicas irracionales
Las ecuaciones
irracionales son aquellas que tienen al menos un polinomio bajo el signo
radical.
2.
Ecuaciones no polinómicas
2.1 Ecuaciones exponenciales
Son ecuaciones en la que
la incógnita aparece en el exponente.
2.2 Ecuaciones logarítmicas
Son ecuaciones en la que la incógnita aparece afectada
por un logaritmo.
2.3
Ecuaciones trigonométricas
Son las ecuaciones en las
que la incógnita está afectada por una función trigonométrica. Como éstas son
periódicas, habrá por lo general infinitas soluciones.





















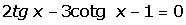



No hay comentarios.:
Publicar un comentario